P==NP 吗

NP/NP-complete/NP-hard，为什么会有这么多看起来长得差不多的东西？我们先来搞清楚，这一大堆东西是干啥的。

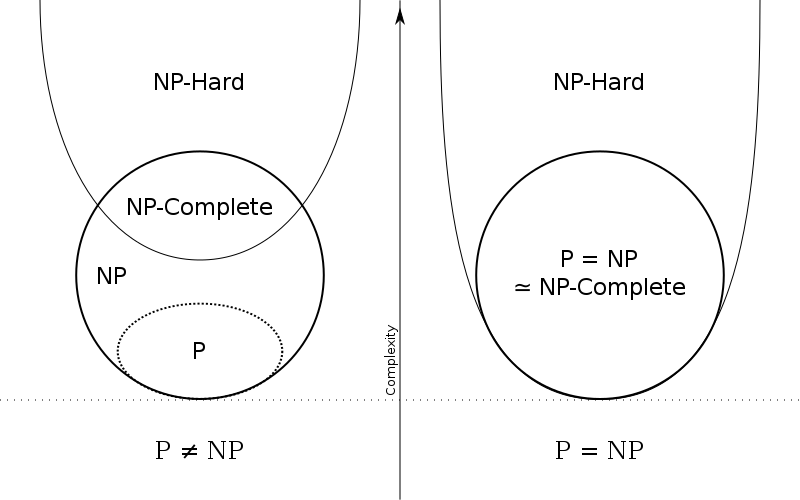
在计算复杂性理论里，我们对一类比较重要的问题的复杂度进行判断。这类问题是 “决定性问题”，简单来说，就是输出只有 “是” 或 “否” 的问题，比如 “3 是不是质数？” 不同的问题有不同的算法，也就有不同的时间复杂度。对于某种算法而言，一般来说，只有它是 “快” 的，才有真正的实用价值。这里的 “快” 指的是多项式时间，缩写为 “P”。注：本段和下一段的时间复杂度均指图灵机模型下的复杂度。

那么 “NP” 就是指 “Non-polynomial” 喽？非也。这样分的话过于粗暴。“NP” 指的是 “Non-deterministic polynomial”，换句话说，如果一个问题不能在多项式时间内给出 “yes” 或 “no” 的解（也许只是没找到），但是如果给出一个 “yes” 的解，算法可以在多项式时间内验证这个解的正确性，那么我们把这类问题归为 “NP” 问题。事实上这种 “求解难，验证容易” 的问题非常常见，比如求解数独游戏，比如判断版的 “旅行商问题”。

emmm 事实上，关于 P 和 NP，还有另一种解释。“P” 指的是 “deterministic Turing machine (DTM)”（wdnmd 不会翻译）可以在多项式时间内给出解的问题，“NP” 指的是 “non-deterministic Turing machine (NTM)” 可以在多项式时间内给出解的问题。那 NTM（不是骂人）可是好东西啊，压缩时间复杂度的无敌利器！想多了，这玩意就不存在，只是一个理论模型。你来看看它是怎么工作的：

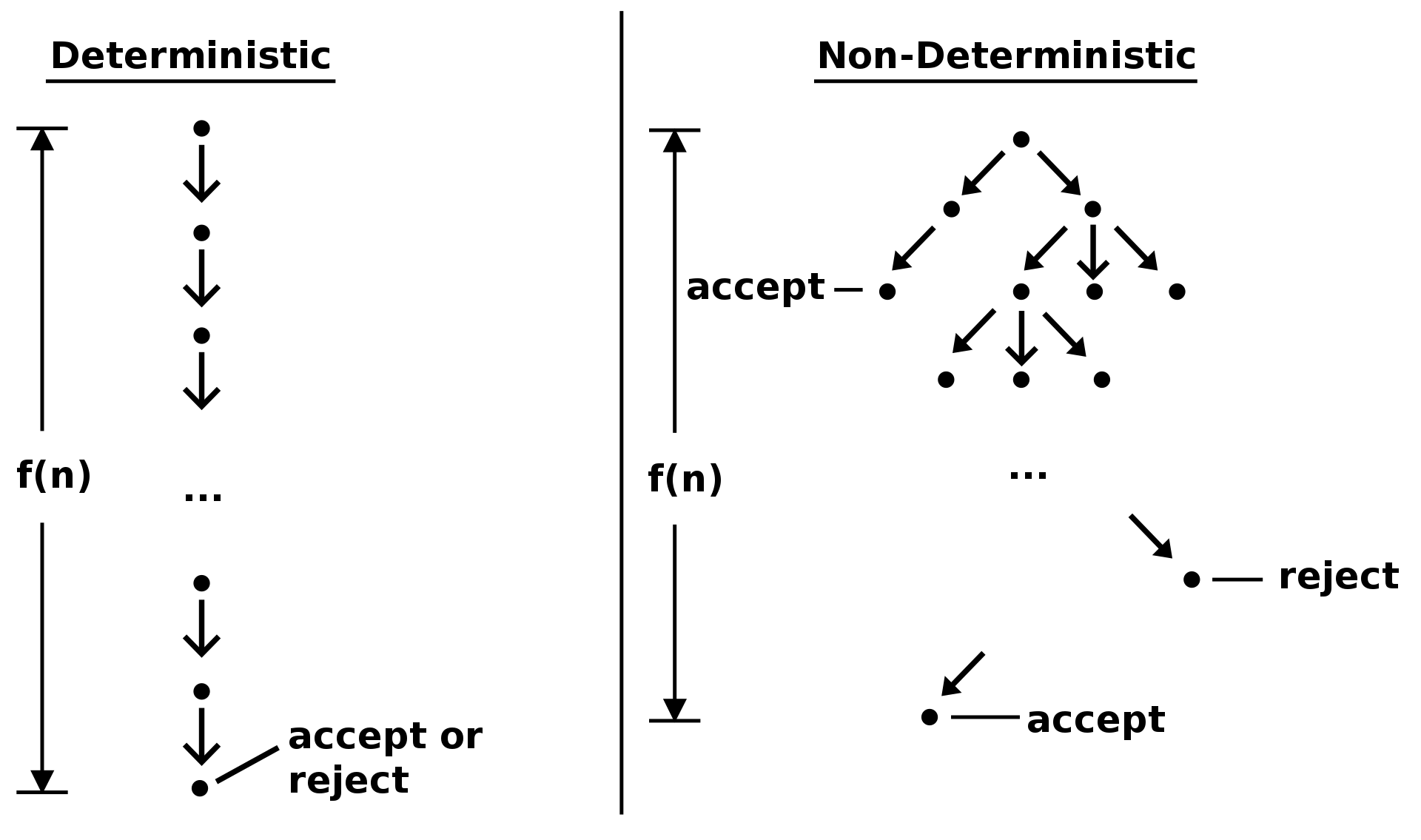
这是两种图灵机的运行模型，一目了然。那 NTM 怎么知道自己该走哪条路呢？1. 我牛逼，每次都走最对的那条；2. 小孩子才做选择，我牛逼，有几条路我就同时走几条路。

那么为什么会出现 NTM 这种听起来这么不靠谱的模型呢？-- 直到现在都没法被实现的那种。我认为原因有二：在理论层面这确实是一种计算模型，不同于 DTM 的模型；解决 P=NP？的问题。（以上仅为个人推测，未查找文献）。

那么回到 P=NP? 这个问题本身（好像之前就没说过），问题的描述很清晰，看那两个 Venn 图就行了。我们再重新看一下 NP 问题的定义（在图灵机下的定义），这里并没有提到 NP 问题的解是否能在多项式时间内被找到。为什么呢？如果确定能找到，那么 P=NP，如果确定找不到，那么 P≠NP。而现在的情况是：不知道能不能找到，但是目前没找到（没找到不代表不存在，对吧？）。

所以 P=NP? 这个问题本身还是非常重要的，直接被列入了克雷研究所提出的千禧年的七大问题之一。毕竟从理论上给了定论了啊，不相等的话就别瞎费劲了，怎么努力也找不到多项式时间内的算法；相等的话就令人激动了，说明现在方向可能不对，而理论计算模型领域可能有一片尚未被发现的美景。